Next: 5.4 Adjoint Representation Up: 5 Sim(2) Previous: 5.2 Lie Algebra
The exponential map from
![]() to
to
![]() has a closed form:
has a closed form:
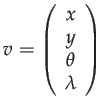 |
(59) | ||
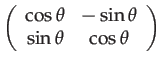 |
(60) | ||
| (61) | |||
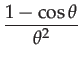 |
(62) | ||
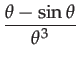 |
(63) | ||
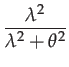 |
(64) | ||
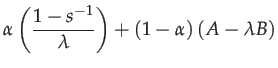 |
(65) | ||
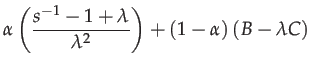 |
(66) | ||
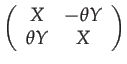 |
(67) | ||
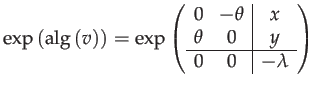 |
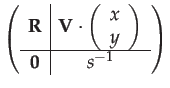 |
(68) |
The elements of
![]() should be calculated with Taylor series
when
should be calculated with Taylor series
when ![]() or
or ![]() is small.
is small.
Ethan Eade 2012-02-16