Next: 10.4 Adjoint Representation Up: 10 Sim(3) Previous: 10.2 Lie Algebra
The exponential map from
![]() to
to
![]() has a closed form:
has a closed form:
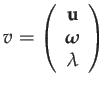 |
(135) | ||
| (136) | |||
| (137) | |||
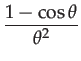 |
(138) | ||
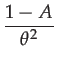 |
(139) | ||
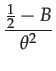 |
(140) | ||
| (141) | |||
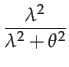 |
(142) | ||
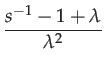 |
(143) | ||
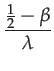 |
(144) | ||
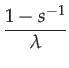 |
(145) | ||
| (146) | |||
| (147) | |||
| (148) | |||
| (149) | |||
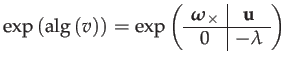 |
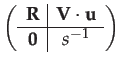 |
(150) |
The coefficients of
![]() and
and
![]() should be calculated
with Taylor series when
should be calculated
with Taylor series when ![]() or
or ![]() is small.
is small.
Ethan Eade 2012-02-16