7.4 Adjoint Representation

First we treat elements of $\mathrm{\mathfrak{sl}}(3)$ , which are $3\times3$ matrices, as 9-vectors, writing the entries in row-major order. Then, for $h\in\mathrm{\mathfrak{sl}}(3)$ and $\mathbf{H}\in\mathrm{SL}(3)$ , the conjugation $\mathbf{H}\cdot h\cdot\mathbf{H}^{-1}$ can be expressed as a linear mapping $\mathbf{C}_{\mathbf{H}}$ on the elements of

. Pre- and post- applying matrix representations of $\mathrm{alg}$ and $\mathrm{alg}^{-1}$ respectively then gives the adjoint representation.

$\displaystyle \left[\mathrm{alg}\right]$	$\displaystyle \equiv$	$\displaystyle \left(\begin{array}{cccccccc} 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0\\ 0 ... ... 1\\ 0 & 0 & 0 & -2 & 0 & 0 & 0 & 0 \end{array}\right)\in\mathbb{R}^{9\times8}$	(88)
$\displaystyle \left[\mathrm{alg}^{-1}\right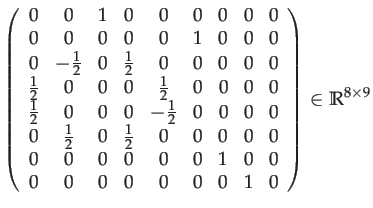]$	$\displaystyle \equiv$	$\displaystyle \left(\begin{array}{ccccccccc} 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\... ...\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \end{array}\right)\in\mathbb{R}^{8\times9}$	(89)
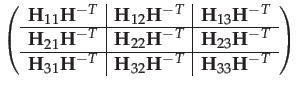$\displaystyle \mathbf{C}_{\mathbf{H}}$	$\displaystyle \equiv$	$\displaystyle \left(\begin{array}{c\vert c\vert c} \mathbf{H}_{11}\mathbf{H}^{-... ...thbf{H}_{32}\mathbf{H}^{-T} & \mathbf{H}_{33}\mathbf{H}^{-T} \end{array}\right)$	(90)

$\displaystyle \mathrm{Adj}_{\mathbf{H}}$

$\displaystyle =$

$\displaystyle \left[\mathrm{alg}^{-1}\right]\cdot\mathbf{C}_{\mathbf{H}}\cdot\left[\mathrm{alg}\right]$

(91)