2.5 Adjoint Representation

Consider tangent vectors $a,b\in\mathfrak{g}$ and a group element $X\in\mathrm{G}$ . How can we choose

such that the following relation holds?

$\displaystyle \exp\left(b\right)\cdot X=X\cdot\exp\left(a\right)$

(11)

$\displaystyle \exp\left(b\right)=X\cdot\exp\left(a\right)\cdot X^{-1}$

(12)

$\displaystyle b=\log\left(X\cdot\exp\left(a\right)\cdot X^{-1}\right)$

(13)

In fact, the identical result can be obtained by using the adjoint representation. A group $\mathrm{G}\subset\mathbb{R}^{n\times n}$ with

degrees of freedom has an isomorphic representation as the group of linear transformations on $\mathfrak{g}$ , called the adjoint:

$\displaystyle X$	$\displaystyle \in$	$\displaystyle \mathrm{G}$	(14)
$\displaystyle a$	$\displaystyle \in$	$\displaystyle \mathfrak{g}$	(15)
$\displaystyle \mathrm{Adj}_{X}:\mathfrak{g}$	$\displaystyle \rightarrow$	$\displaystyle \mathfrak{g}$	(16)
$\displaystyle \mathrm{Adj}_{X}\left(a\right)$	$\displaystyle =$	$\displaystyle X\cdot a\cdot X^{-1}\in\mathfrak{g}$	(17)

Elements of the adjoint representation are usually written as $k\times k$ matrices acting on the coefficient vectors of elements in $\mathfrak{g}$ by multiplication.

$\displaystyle X,Y$	$\displaystyle \in$	$\displaystyle \mathrm{G}$	(18)
$\displaystyle \mathrm{Adj}_{X\cdot Y}$	$\displaystyle =$	$\displaystyle \mathrm{Adj}_{X}\cdot\mathrm{Adj}_{Y}$	(19)
$\displaystyle \mathrm{Adj}_{X^{-1}}$	$\displaystyle =$	$\displaystyle \mathrm{Adj}_{X}^{-1}$	(20)

$\displaystyle b$	$\displaystyle \equiv$	$\displaystyle \mathrm{Adj}_{X}\left(a\right)$	(21)
$\displaystyle \implies\exp\left(b\right)$	$\displaystyle =$	$\displaystyle X\cdot\exp\left(a\right)\cdot X^{-1}$	(22)
$\displaystyle \implies\exp\left(b\right)\cdot X$	$\displaystyle =$	$\displaystyle X\cdot\exp\left(a\right)$	(23)

Thus the adjoint is effectively the Jacobian of the transformation of tangent vectors through elements of the group:

$\displaystyle \mathbf{c}$	$\displaystyle \in$	$\displaystyle \mathbb{R}^{k}$	(24)
$\displaystyle X$	$\displaystyle \in$	$\displaystyle \mathrm{G}$	(25)
$\displaystyle f:\mathrm{G}\times\mathbb{R}^{k}$	$\displaystyle \rightarrow$	$\displaystyle \mathbb{R}^{k}$	(26)
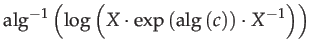$\displaystyle f(X,\mathbf{c})$	$\displaystyle =$	$\displaystyle \mathrm{alg}^{-1}\left(\log\left(X\cdot\exp\left(\mathrm{alg}\left(c\right)\right)\cdot X^{-1}\right)\right)$	(27)
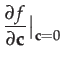$\displaystyle \frac{\partial f}{\partial\mathbf{c}}\big\vert _{\mathbf{c}=0}$	$\displaystyle =$	$\displaystyle \mathrm{Adj}_{X}$	(28)