2.2 Lie Algebra

Consider a Lie group $\mathrm{G}$ represented in $\mathbb{R}^{n\times n}$, with $k$ degrees of freedom. The Lie algebra $\mathfrak{g}$ is the space of differential transformations - the tangent space - around the identity of $\mathrm{G}$. This tangent space is a $k$-dimensional vector space with basis elements $\left\{ G_{1},\ldots,G_{k}\right\}$: the generators. Elements of $\mathfrak{g}$ are represented as matrices in $\mathbb{R}^{n\times n}$, but under addition and scalar multiplication, rather than matrix multiplication.

For such a Lie algebra $\mathfrak{g}$, we write the linear combination of generators $\left\{ G_{i}\right\}$ specified by a vector of coefficients $\mathbf{c}$ as $\mathrm{alg}\left(\mathbf{c}\right)$:

$$\mathrm{alg}:\mathbb{R}^{k} \rightarrow \mathfrak{g}\subset\mathbb{R}^{n\times n}$$ (1)

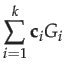$$\mathrm{alg}\left(\mathbf{c}\right) \equiv \sum_{i=1}^{k}\mathbf{c}_{i}G_{i}$$ (2)

We denote the unique inverse of this linear combination by $\mathrm{alg}^{-1}$. It might seem confusing that a tangent vector is in fact an $n\times n$ matrix, but it can always be thought of (and represented) as the vector of coefficients of the generators.