2.3 Exponential Map and Logarithm

The exponential map takes elements in the algebra to elements in the group. Intuitively speaking, it walks along the group manifold in the differential direction specified by the tangent vector in the algebra. For matrix groups the exponential map is simply matrix exponentiation:

$$\exp:\mathfrak{g} \rightarrow \mathrm{G}$$ (3)

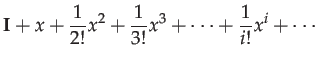$$\exp\left(x\right) = \mathbf{I}+x+\frac{1}{2!}x^{2}+\frac{1}{3!}x^{3}+\cdots+\frac{1}{i!}x^{i}+\cdots$$ (4)

For several groups described below, the exponential map has a closed form. It is always a continuous map.

The inverse of the exponential map is the logarithm:

$$\exp\left(\log\left(X\right)\right) = X$$ (5)

The logarithm is usually not continuous everywhere, but is always continuous near the identity. Note that for most groups, including all groups with compact subgroups such as rotations, neither $\exp$ nor $\log$ is injective.